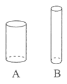
用一张长18.84cm,宽12.56cm的长方形纸围成一个圆柱的侧面,可以有A、B两种不同的用法(如图)。A圆柱与B圆柱体积的最简单整数比是________:________。
【答案】3 2
【解析】
观察图可知,圆柱A的底面周长是18.84cm,高是12.56cm,先求出圆柱的底面半径,用底面周长÷2÷π=底面半径,然后用公式:V=πr2h,求出圆柱A的体积;圆柱B的底面周长是12.56cm,高是18.84cm,先求出圆柱的底面半径,用底面周长÷2÷π=底面半径,然后用公式:V=πr2h,求出圆柱A的体积;然后用圆柱A的体积与圆柱B的体积,据此化简为最简整数比即可.
A圆柱:底面周长是18.84cm,高是12.56cm,
底面半径:
18.84÷2÷3.14
=9.42÷3.14
=3(cm)
体积:
π×32×12.56
=π×9×12.56
=113.04π(cm3)
B圆柱:底面周长是12.56cm,高是18.84cm,
底面半径:
12.56÷2÷3.14
=6.28÷3.14
=2(cm)
体积:
π×22×18.84
=π×4×18.84
=75.36π(cm3)
A圆柱的体积:B圆柱的体积=113.04π:75.36π=113.04:75.36=(113.04×100):(75.36×100)=11304:7536=(11304÷3768):(7536÷3768)=3:2.
故答案为:3;2.





