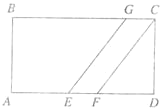
如图,长方形ABCD中有两条平行线,将它分成了一个梯形AEGB、平行四边形EFCG和三角形FDC。AE:EF:FD=2:1:2,那么梯形、平行四边形、三角形面积的比是________。
【答案】3:1:1
【解析】
长方形的对边相等,根据条件“ AE:EF:FD=2:1:2 ”可知,把AE看作2份,EF看作1份,FD看作2份,求出BG的长度,然后设长方形的宽是h,则梯形AEGB、平行四边形EFCG、三角形FDC的高也是h,依据梯形的面积=(上底+下底)×高÷2,平行四边形的面积=底×高,三角形的面积=底×高÷2,写出它们的面积,然后化简它们的面积比,据此解答.
BG=AE+DF=2+2=4;
设长方形的宽是h,则梯形AEGB、平行四边形EFCG、三角形FDC的高也是h,
梯形、平行四边形、三角形面积的比是:
(2+4)×h÷2:1×h:2×h÷2
=6h÷2:h:h
=3h:h:h
=3:1:1.
故答案为:3:1:1.





